Public key cryptography

Public-key cryptography (asymmetric cryptography) is a subdomain of cryptography that deals with public-private key pairs.

What does that even mean? and why is it useful?

Analogy

Here's a helpful analogy for PKC that I came up with back when I was learning about this technique. Imagine you're taking a stroll down a neighborhood and you find a house you like. You take out a random key and try to insert it into the keyhole; probably won't work right? You need a key (private key) that is compatible with the lock (public key). Notice that the lock (public key) is available to everyone to interact with, but the key is always kept private by the owner.

This is how PKC works (kind-of).

Deep dive

The public key is derived from the private key and not vice versa. This is done using a method called elliptic curve multiplication:

Inversion of this operation isn't as simple as dividing . Solving for the private key in this scenario requires finding the discrete logarithm, which is computationally infeasible for a large enough key.

Note: The elliptic curve space does not allow divisions, allowing only one-way multiplication.

One of the most common types of elliptic curves used today is the secp256k1 which is defined by,

indicates that the curve is defined over a finite field of prime order , where , which is a very large prime.

The multiplicity of produces a seemingly random point on the elliptic curve. Guessing the multiplier for a high prime order is computationally infeasible due to difficulty.

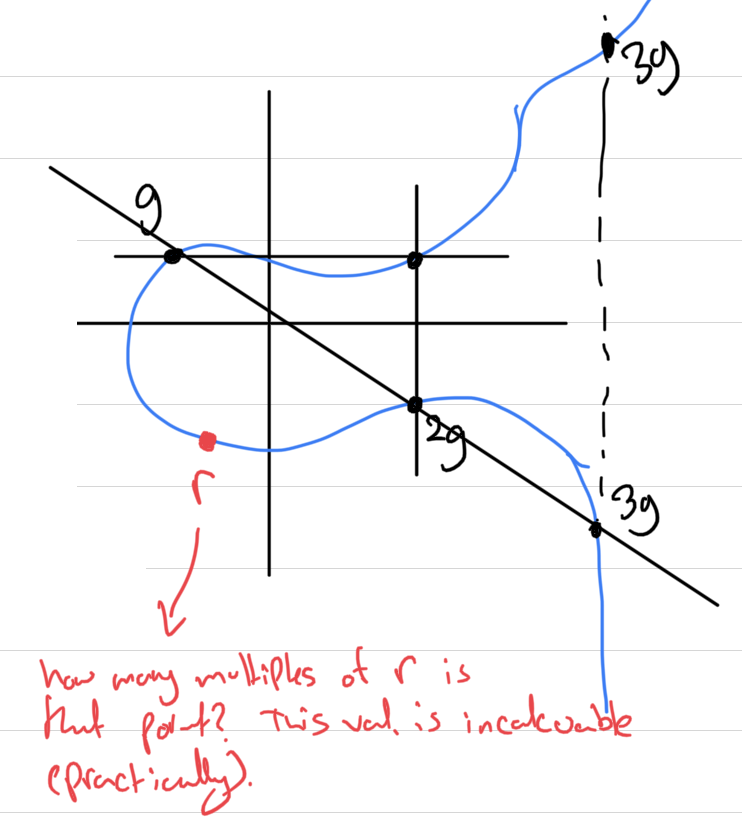
Elliptic curve addition is defined by , where is also on the elliptic curve. Geometrically, a straight line is drawn between & which will intersect the curve in one additional place, . , then reflect in the x-axis to get .