← go back

Topological spaces and Manifolds

Cover Image for Topological spaces and Manifolds

Definition

A topological space is a fundamental concept in the field of topology, a branch of mathematics concerned with the properties of space that are preserved under continuous transformations. Formally, a topological space is defined by a set of points and a set of subsets of , known as the critical neighbourhoods , for each point. These neighbourhoods help us understand the local structure of the space.

Axioms of Topology

Topological spaces adhere to the following axioms:

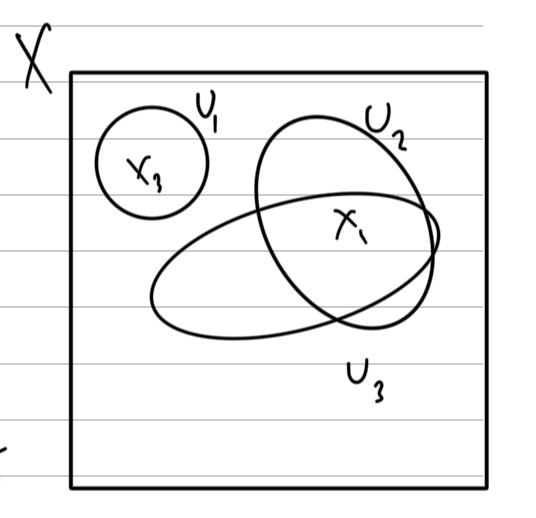
  1. Inclusion of Point in Neighbourhood: If is a neighbourhood of (), then is an element of .
  2. Neighbourhood Containment: If and , and is a neighbourhood of , then is also a neighbourhood of .
  3. Intersection Property: The intersection of two neighbourhoods of is also a neighbourhood of .
  4. Neighbourhood of Neighbourhood: Any neighbourhood of includes a neighbourhood of such that is a neighbourhood of all points in .

Homeomorphism

A function between two topological spaces is a homeomorphism if it satisfies three conditions:

  1. Bijection: is one-to-one and onto.
  2. Continuity: does not tear or glue the space; it's a smooth transformation.
  3. Inverse Continuity: The inverse function is also continuous.

diag1

When such a function exists, we say and are homeomorphic, or topologically equivalent. This means they have the same shape or structure from a topological viewpoint, even if they look different geometrically.

The Role of Manifolds in Topology

Manifolds are a special class of topological spaces that locally resemble Euclidean space. A topological space is a manifold if, for all points , there exists a neighbourhood of and some integer such that is homeomorphic to a subset of . The smallest such is called the dimension of the manifold. Manifolds are crucial in understanding complex shapes and forms in higher dimensions and have applications in physics, engineering, and beyond.

Understanding topological spaces and their properties is essential in the realm of advanced mathematics and theoretical physics. They offer a framework to study continuous transformations and intrinsic properties of spaces, irrespective of their exact shape or size.